�@��2����u���i2018/6/16�j
�]�˂̐��w�u�a�Z�v�Ƀ`�������W
�c�{�E�`�m�E�m���@�ؓ� �a�r�@
�m�{�L���́A���w�Ձx��4����背�C�A�E�g��ύX���Čf�ڂ��Ă��܂��n�@
1.�͂��߂�
�@���y���R���ォ��]�ˎ��㏉�߁i�����ȑO�j�ɂ����āA�����Ŗ|�ꂽ���m�̓V���w�␔�w�����{�ɓ����Ă������Ƃɂ��A �]�ˎ���ɂ͓��{�Ǝ��̐��w�����W�����B�u�a�Z�v�̌Ăі��́A�����ȍ~�ɐ��m���w�Ƌ�ʂ��邽�߂Ɏg�p�����悤�ɂȂ������̂ŁA �����́u�Z�p�v�ȂǂƌĂ�Ă���A�w��Ƃ������͐����̒��Ŗ𗧂u���w�v�Ƃ��Ă̈Ӗ����������������B
�y�֍F�a�̏ё���z�i���{�w�m�@�����j

�}-1 �g�c���R�w�o���L�x1631�N
�i�������������ُ����j

�}-2 �w�V�Ґo���L�x�i��������}���ُ����j
�@�a�Z�̕��y�ɑ傫�Ȗ�����S�����̂��A�g�c���R�i1598�`1672�j�̍]�ˏ����ɔ��s�����u�o���L�v�ł���B �P�ɂ����̉���ɂƂǂ܂炸�A���i�������܂ށj�̐��������ォ��n�܂�A���ۂ̐����̒��Ŗ𗧂v�Z�@ �i���i�̔��蔃���E�����̊��Z�E�c���̑��ʂȂǁj�ɉ����A�p�q(�܂܂�)���āE�ߋT�Z�E�l�Z�E�U���Z�Ȃǐ��w�V�Y�I�Ȗ��܂Ōf�ڂ����B ���ꂪ��x�X�g�Z���[�ƂȂ�A���m�����łȂ��A���l��_���ɂ܂Ő��w���L���錳�ƂȂ����B ���R���g���o�ł����̂�4���ł���i�}-1�j���A���̌�ގ��{���������s����i�}-2�j�A���i���疾���Ɏ���250�N���̊ԓǂݑ�����ꂽ�B
2.�㐔�I���
�i1�j�ߋT�Z
�@���Ƃ��Ƃ́A�����̏�����賂Ɠe���g���Ă������A����12�N�i1815�j���납����{�l�ɂȂ��݂̐[���߂ƋT�ɂȂ����ƌ����Ă���B���L賓e���ā@��L�O�\�ܓ��@���L��\�l���@��賓e�e��
�@賂Ɠe�������Ăɓ����Ă���B�ォ�猩��Ɠ���35������A�����猩��Ƒ���94���������B賂Ɠe�͂��ꂼ�ꉽ�H���邩�H
�y����̉������i�A���������j�z
賂̐��� \(x\) �H�A�e�� \(y\) �H�Ƃ���B���̐��̊W����@�@ \(x+y=35 \cdots\) �@
���̐��̊W����@�@ \(2x+4y=94 \cdots\) �A
�A�|�@�~2���@�@�@�@ \(2y=24\)
����ā@�@�@�@�@�@�@�@\(y=12\)
�܂��A�@���@�@�@�@�@\(x=23\)
�y�a�Z�̉������z
35�H���ׂ�賂Ƃ���ƁA���̐����@�@\(2�~35=70\)
賂�1�H���炵�A�e���P�H���₷���тɑ���2�{����������̂�
�@�@\((94-70)��2=12\)
�œe�̐������܂�B����͘A���������� \(y\) �����߂�Ƃ��̌v�Z
�@�@\(y=24��2=(94-35�~2)��(4-2)\)
�Ɠ������Ƃ����Ă��邱�ƂɂȂ�B
�i�j�@� 23�H�A�e 12�H�@
�i2�j��˂̐[���𑪂�
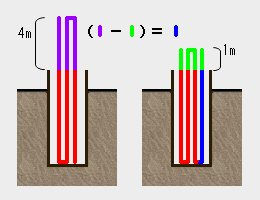
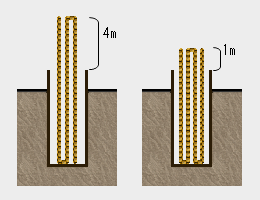 �@���̂Ȃ���˂̐[���𑪂�̂ɓ���g���܂����B���3�����ɂ��đ��˂ē����ƁA4m�]��܂����B
���ɁA4�����ɂ��đ��˂ē����ƁA1m�]��܂����B��˂̐[���Ɠ�̒����͉�m�ł��傤���H
�@���̂Ȃ���˂̐[���𑪂�̂ɓ���g���܂����B���3�����ɂ��đ��˂ē����ƁA4m�]��܂����B
���ɁA4�����ɂ��đ��˂ē����ƁA1m�]��܂����B��˂̐[���Ɠ�̒����͉�m�ł��傤���H
�i��֎s�����فu�a�Z�ɒ���v����26�N�x�j
�y����̉������i�ꎟ�������j�z
��˂̐[���� $x$ m�Ƃ���B3�����������̓�̒����́@�@�@�@ \((x+4)�~3=3x+12 \cdots\) �@
4�����������̓�̒����́@�@�@�@ \((x+1)�~4=4x+4 \cdots\) �A
�@�ƇA�͓���������@�@�@�@�@�@�@ \(3x+12=4x+4\)
����������āA��˂̐[���́@�@�@ \(x=8\)�im�j
��̒����́@�@�@�@�@�@�@�@�@�@�@ \((8+4)�~3=36\)�im�j
�y�a�Z�̉������z
��˂̏�ɏo�Ă��镔���̒����̈Ⴂ���@\(4�~3-1�~4=12-4=8\)
����͈�˂̒��ɂ����̒����̍��ɓ������B���̖��ł́A��˂̒��ɂ����̒����̍��� ��˂̐[���ɓ������̂ŁA��˂̐[����8m�ł���
�i�j�@��˂̐[��8m�@��̒���36m�@
�i3�j�U���Z*1)
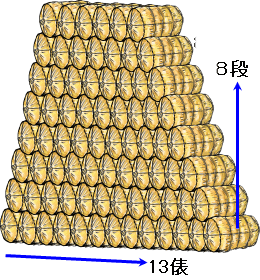
�@�E�}�̂悤�ɕU��ςݏグ�Ă����B�ʼn��i�̕U��13�ŁA������8�i�̎��A�U�͑S���ʼn����邩�B�y����̉������i����̘a�j�z
1�i�ςނ��ƂɕU�̐���1���������U�̑����� \(S\) �Ƃ����
�@\(S=13+12+ \cdots +6\dots�@\)
��̒i���瑫���Ă�����
�@\(S=6+7+ \dots +13\dots�A\)
�@�{�A \[2S=\overset{8�i}{\overparen{(13+6)+(12+7)+ \dots +(6+13)}}\] \[S= \dfrac{\overset{8�i}{\overparen{(13+6) \dots +(6+13)}}} {2}= \dfrac{9�~8} {2}=76\]

�y�a�Z�̉������z
�@�E�}�̂悤�ɁA�㉺���]�������̂���ׂ�ƕ��s�l�ӌ`�ɂȂ�B���̎��A1�i�̕U�̐��́A�i�ŏ�i�̐��j�{�i�ʼn��i�̐��j
�ƂȂ�̂ŁA�@�@�@�@�@ \(6�{13��19 \)�i�U�j
�]���āA�U�̑����́@�@ \(19�~8��2��76 \)
���̎��́A��������̘a�̌����ɂ��v�Z�ƑS�������ł���B
�@�@�i�j�@76�U�@
��1)�U���Z
�@�U��ςݏグ�āA�O�p�`�ɂ����Ƃ��ɐ��̖̂悤�Ȍ`�ɂȂ邱�Ƃ��炱�̖��O���t����ꂽ�Ƃ�����B
�@�U��ςݏグ�āA�O�p�`�ɂ����Ƃ��ɐ��̖̂悤�Ȍ`�ɂȂ邱�Ƃ��炱�̖��O���t����ꂽ�Ƃ�����B
�i4�j�ő���ƍŏ����{��
�@���L�ώ펪�s�m���ΐ��@���]��l�l�����������]���]�l�l���������]�@��ΐ����p�@��
�@�ς�����܂��B���̐�(����)���͂킩��Ȃ��B�����A2�l4�����܂��Ɨ]�肪�Ȃ������B
�܂��A4�l2���������Ă��]�肪�Ȃ������B���ΐ��͂ǂꂾ�����B�ł��������l�����߂�B
�i�������O�t���@��א_�Ё@�����j
�y����̉������i�ŏ����{�������߂�j�z
�@2�l4����24���A�@4�l2����42���@������A2�̐���24��42�̍ŏ����{�������߂邱�ƂɂȂ�B
2�@�j24�@�@42�@
3�@�j12�@�@21�@
�@ 4�@�@ 7
����āA�ŏ����{���́@�@ \(2�~3�~4�~7��168\)
3�@�j12�@�@21�@
�@ 4�@�@ 7
�y�a�Z�̉������z
�ő�������̂悤�ɋ��߂�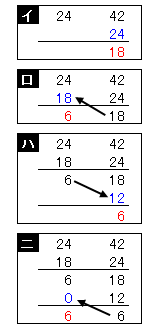
- 2�̐�����ׁA�傫����42���珬������24�������B
- 24����c����18�̔{���i24���傫���Ȃ�Ȃ��{���A���̏ꍇ��1�{��18�j�������B
- 18����c����6�̔{���@�i�]�肪0�ɂȂ�1�O�A���̏ꍇ��2�{��12�j�������B
- �n�̏ꍇ�Ɠ��l�ɁA����6����E��6�̔{���i���̏ꍇ��0�{��0�j�������B
- �c�������������ɂȂ�����A���̐����ő���ƂȂ�B
�ŏ����{���́A���̎��i����A�j���狁�߂�B
\(\dfrac{(���P)}{(�ő����)}�~\dfrac{(���Q)}{(�ő����)}�~(�ő����)\)
�@�@�@�@\( \dfrac{24}{6}�~\dfrac{42}{6}�~6=4�~7�~6=168\)
�@�@�@�@�i�j�@1��6�l8���@
�@�ǂ���̕��@�ł��A�ŏI�I�ɂ� \(6�~4�~7\) ���v�Z���Ă��邱�Ƃ��킩��B
�@�Ȃ��A����A�͌��݂ł����Z�̐��w�Ŏg��������ł���B
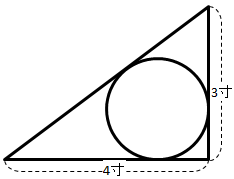
3.�I���
�i1�j���p�O�p�`�Ɠ��ډ~
�@���p�O�p�`�ɁA�~�����ڂ��Ă���B���p�O�p�`�̒��p������2�ӂ̒������A3����4���̎��A�~�̒��a�͂ǂꂾ�����H�y�ʐς���̉������z
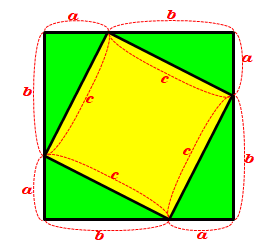
�܂��A���p�O�p�`�̎Εӂ̒��������߂�B�O�����̒藝*2)�Ł@ \(\overline{AB}^2=\overline{BC}^2+\overline{CA}^2\)
������@�@�@�@�@\(\overline{AB}\) \(= 5\)�i���j�@�ƂȂ�B
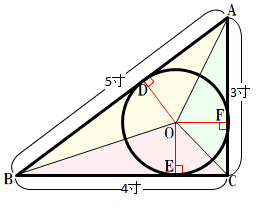 �@�E�}�̂悤�ɁA���ډ~�̒��S \(O\)�Ɗe�ӂ̐ړ_ \(D�AE�AF\) �����ԁB
�@�E�}�̂悤�ɁA���ډ~�̒��S \(O\)�Ɗe�ӂ̐ړ_ \(D�AE�AF\) �����ԁB�_ \(O\) �_�Ƃ��� \(��AOB�A��BOC�A��COA\) �̖ʐς̘a�� \(��ABC\) �ɓ������A ���̍��� \(\overline{OD}�A\overline{OE}�A\overline{OF}\) �͓��ډ~�̔��a�ł���S�ē������B
�@\(\dfrac{(AB�~OD)} {2} + \dfrac{(BC�~OE)} {2}+ \dfrac{(AC�~OF)} {2}= \dfrac{(BC�~AC)} {2} \)
\((\overline{AB}+\overline{BC}+\overline{AC})\)\(�~\)(���a)\(=\)\(\overline{BC}�~\overline{AC}\)
\((5+4+3)�~\)(���a)\(=4�~3\)
�@�@ ���a��1�i���j
�y�ڐ��̒�������̉������z
\(\overline{AD}=\overline{AF}�A\overline{BD}=\overline{BE}�A\overline{CE}=\overline{CF}\) ���\(\overline{AB}=\overline{AD}+\overline{BD}\)
�@�@\(=\overline{AF}+\overline{BE}\)
�@�@\(=(\overline{AC}-\overline{CF})+(\overline{BC}-\overline{CE})\)
����ā@\(\overline{CE}+\overline{CF}=\overline{AC}+\overline{BC}-\overline{AB}\)
�����ŁA \(\overline{CE}=\overline{OF}=\overline{OE}=\overline{CF}=\)�i���a�j
�@�i�l�p�` \(OECF\) �͔��a����ӂƂ��鐳���`�j
\(\overline{CE}+\overline{CF}\)�i���a�j\(=\overline{AC}+\overline{BC}-\overline{AB}=\)\(3+4-5=2\)
�@�@�i�j���a��2���@
�@�a�Z�ł́A��̍l�������瓱���o���ꂽ��
���ډ~�̒��a \(=\overline{BC}+\overline{CA}-\overline{AB}\)
�������Ƃ��Ă悭�p�����Ă���B�i2�j�����ɐڂ���2�~
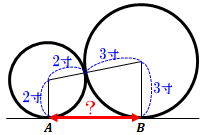 �@�E�}�̂悤�ɒ����ɔ��a3���̑�~�Ɣ��a2���̏��~���_ \(A�AB\) �Őڂ��Ă���B�܂��A�~���m���ڂ��Ă���B
���̎��A�ړ_�Ԃ̋��� \(AB\) �͂ǂꂾ���ɂȂ邩�H
�@�E�}�̂悤�ɒ����ɔ��a3���̑�~�Ɣ��a2���̏��~���_ \(A�AB\) �Őڂ��Ă���B�܂��A�~���m���ڂ��Ă���B
���̎��A�ړ_�Ԃ̋��� \(AB\) �͂ǂꂾ���ɂȂ邩�H
�y�������z
�@�}�̂悤�ɁA�~�̒��S \(O�AP\) �����Ԑ������ΕӂƂ��钼�p�O�p�` \(OPQ\) �����B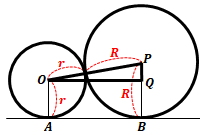 �O�����̒藝����
�O�����̒藝�����@\(\overline{OP}^2=\overline{OQ}^2+\overline{PQ}^2\)
���~�̔��a�� \(r\)�A��~�̔��a�� \(R\) �Ƃ���ƁA
\(\overline{OQ}^2\)\(=(R+r)^2-(R-r)^2\)
�@�@ \(=R^2+2rR+r^2-R^2+2rR-r^2\)
�@�@ \(=4rR\)
����ā@�@ \(\overline{AB}=\overline{OQ}\)\(=\sqrt{4�~2�~3}=\sqrt{24}=2\sqrt{6}\)
�@�@�@�i�j \(2\sqrt{6}\) ���@
�@ �]�ˎ���ɂ��A��̍l�������瓱�����
\(\overline{AB}=\sqrt{D_1D_2}\) �@�i \(D_1,D_2\) ��2�~�̒��a�j
�������Ƃ��Ďg���Ă���*3)�B
��2)�O�����̒藝�i�s�^�S���X�̒藝�j
 �@BC2���I����A���ɒ����ł́w��鏎Z�o�x�ŁA���̒藝�������Ă���A��Ҍ��̖@�ƌĂ�A
���{�ɓ`�����Ă�����������̂��g���Ă��܂����B���̒藝�̏ؖ��@�͐��S�ʂ肠��Ƃ����Ă��܂����A
���̉E�}�͂��̑�\�I�ȗ�œ�̎l�p�̖ʐς���ؖ��ł��܂��B
�@BC2���I����A���ɒ����ł́w��鏎Z�o�x�ŁA���̒藝�������Ă���A��Ҍ��̖@�ƌĂ�A
���{�ɓ`�����Ă�����������̂��g���Ă��܂����B���̒藝�̏ؖ��@�͐��S�ʂ肠��Ƃ����Ă��܂����A
���̉E�}�͂��̑�\�I�ȗ�œ�̎l�p�̖ʐς���ؖ��ł��܂��B
 �O���̎l�p�̖ʐς́B�����̎l�p�i���j��4�̎O�p�i�j�����������̂Ɠ����Ȃ̂�
�O���̎l�p�̖ʐς́B�����̎l�p�i���j��4�̎O�p�i�j�����������̂Ɠ����Ȃ̂�
�@�@\((a+b)^2=c^2\)(��)\(+ \dfrac{ab}{2}\)(��)\(�~4\)
�@�@ \((a+b)^2-2ab=c^2\)
�@�@ \(a^2+b^2=c^2\)
 ��3)������
��3)������
�@�a�Z�ł́A�����������߂邱�Ƃ��u�J������v�Ƃ����Ă��܂����B�������̋L���͂Ȃ������̂Ő��l���J�����āA�ߎ��l���L�q���Ă��܂����B �܂��A�u��144�̕��ʂ�12�v�Ƃ����悤�ȋL�q���݂��܂��B �֍F�a�̖T���@�ł͉E�̂悤�ɕ\�L���Ă����悤�ł��B
 �@�����������߂�ꍇ�́A������Z���g���Ă��܂������A���̍l�����Ƃ��Ă͉E�}�̂悤�ɖʐς�z�肵�Ȃ���
���ɉ��̈ʂ����߂Ă����܂��B
�@�����������߂�ꍇ�́A������Z���g���Ă��܂������A���̍l�����Ƃ��Ă͉E�}�̂悤�ɖʐς�z�肵�Ȃ���
���ɉ��̈ʂ����߂Ă����܂��B
��Ƃ��ā@\(\sqrt{15129}=123\) �����߂Ă��܂��B
 �@BC2���I����A���ɒ����ł́w��鏎Z�o�x�ŁA���̒藝�������Ă���A��Ҍ��̖@�ƌĂ�A
���{�ɓ`�����Ă�����������̂��g���Ă��܂����B���̒藝�̏ؖ��@�͐��S�ʂ肠��Ƃ����Ă��܂����A
���̉E�}�͂��̑�\�I�ȗ�œ�̎l�p�̖ʐς���ؖ��ł��܂��B
�@BC2���I����A���ɒ����ł́w��鏎Z�o�x�ŁA���̒藝�������Ă���A��Ҍ��̖@�ƌĂ�A
���{�ɓ`�����Ă�����������̂��g���Ă��܂����B���̒藝�̏ؖ��@�͐��S�ʂ肠��Ƃ����Ă��܂����A
���̉E�}�͂��̑�\�I�ȗ�œ�̎l�p�̖ʐς���ؖ��ł��܂��B �O���̎l�p�̖ʐς́B�����̎l�p�i���j��4�̎O�p�i�j�����������̂Ɠ����Ȃ̂�
�O���̎l�p�̖ʐς́B�����̎l�p�i���j��4�̎O�p�i�j�����������̂Ɠ����Ȃ̂��@�@\((a+b)^2=c^2\)(��)\(+ \dfrac{ab}{2}\)(��)\(�~4\)
�@�@ \((a+b)^2-2ab=c^2\)
�@�@ \(a^2+b^2=c^2\)

�@�@\(\sqrt{5}\)�@�@�@�@�@\(\dfrac{\sqrt{3}+1}{2}\)
�@�a�Z�ł́A�����������߂邱�Ƃ��u�J������v�Ƃ����Ă��܂����B�������̋L���͂Ȃ������̂Ő��l���J�����āA�ߎ��l���L�q���Ă��܂����B �܂��A�u��144�̕��ʂ�12�v�Ƃ����悤�ȋL�q���݂��܂��B �֍F�a�̖T���@�ł͉E�̂悤�ɕ\�L���Ă����悤�ł��B
 �@�����������߂�ꍇ�́A������Z���g���Ă��܂������A���̍l�����Ƃ��Ă͉E�}�̂悤�ɖʐς�z�肵�Ȃ���
���ɉ��̈ʂ����߂Ă����܂��B
�@�����������߂�ꍇ�́A������Z���g���Ă��܂������A���̍l�����Ƃ��Ă͉E�}�̂悤�ɖʐς�z�肵�Ȃ���
���ɉ��̈ʂ����߂Ă����܂��B��Ƃ��ā@\(\sqrt{15129}=123\) �����߂Ă��܂��B
- �S�̈ʁF����100�𗧂Ă�
\(15129-100�~100=5129\) �i���j - �\�̈ʁF����20�𗧂Ă�
\(20�~100+20�~20+100�~20=4400\) �i�@�j
\(5129-4400=729\) �i���j - ��̈ʁF����3�𗧂Ă�
\(3�~120+3�~3+120�~3=729\) �i�@�j
\(729-729=0\) �i���j
�i3�j�����w
�@�����w�Ƃ́A�����`�̃}�X�ڂɐ��������A�}�X�̏c�E���E�߂̐��̘a�����ׂē������Ȃ�悤�ɂ������̂ł���B ���{�ł��A���[���b�p�ɗ�炸�������s���A�O���w����O�\���w�܂ł̍�������������A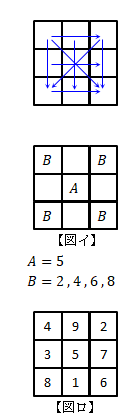 $4�~4�~4$ �̗��̕��w���l�Ă����肵�Ă���B
$4�~4�~4$ �̗��̕��w���l�Ă����肵�Ă���B�@�E�̂悤�� $3�~3$ �̃}�X�ڂ�1�`9�̐�����1������āA�c�E���E�Ίp���̐��̘a�����ׂē������Ȃ�悤�ɂ���B
�y�ʏ�̍l�����z
1�`9�̍��v��45������A1���3�̐��̍��v��\(45��3=15\) �@�ƂȂ�B
3�̐��̍��v��15�ɂȂ�g���l�����
\(�i1�C5�C9�j�i1�C6�C8�j�i2�C4�C9�j�i2�C5�C8�j\)
\(�i2�C6�C7�j�i3�C4�C8�j�i3�C5�C7�j�i4�C5�C6�j\)
��8�ʂ肵���Ȃ��B���̓��A�}�C�� $A$ �ɓ��鐔��4�ʂ�̑g�ݍ��킹�Ɏg����̂ŁA8�ʂ�̂���4��o������g5�h�ł��邱�Ƃ��킩��B ���ɐ}�C�� $B$ �̃}�X�ɓ���̂́A3�ʂ�̑g�ݍ��킹�Ɏg����̂ŁA3��o������ �g2�C4�C6�C8�h �ƂȂ�B �����̑g�ݍ��킹���l���Ĕz�u����ƁA�}���̂悤�ȉ����l������B���ہA��]������A�Ώۈړ������肵�����̂����Ƃ������1�ʂ肵���Ȃ��B �Ƃ��낪�A���̍l�����ł͈�ʓI�ȉ�@�Ƃ͂Ȃ炸�A���̕��w�ɂ͓K�p�ł��Ȃ��B
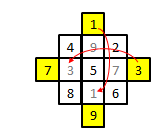
�y�o�V�F�[����*4)�z
�E�̐}�̂悤�ɁA���w�̊O�ɕʂ̃}�X��p�ӂ��A�߂�1�`9�̐��������Ă����B ���ɕ��w�̊O�̃}�X�i���F�œh���������j�̐����A������܂��͍s�̂����Ƃ����ꂽ�Ɉړ�����B�i��j�@1�@���@5�̉��@�@3�@���@5�̍�
����ŁA��̉��Ɠ������̂��ł���B
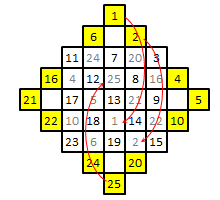
$5�~5$ �̖����w�ł�����Ɠ������@���g����B �������A $4�~4$ �̋����̏ꍇ�͂��̕��@���g���Ȃ��B
�@���݂ɁA4���w��880�ʂ�A5���w��2���ȏ�i275,305,224�j���邱�Ƃ��m���Ă��邪�A6���ȏ�̖����w�̑����͂܂��m���Ă��Ȃ��B
��4)�o�V�F�[����
�o�V�F�[�Ƃ�16���I�̃t�����X�̐��w�҂̖��O�ł����A�a�Z�ł��w���@�x��w���w�V�@�����x�Ȃǂɂ݂邱�Ƃ��ł��܂��B
�o�V�F�[�Ƃ�16���I�̃t�����X�̐��w�҂̖��O�ł����A�a�Z�ł��w���@�x��w���w�V�@�����x�Ȃǂɂ݂邱�Ƃ��ł��܂��B
-
�y�Q�l�����z
- ���R���u�a�Z�̗��j�v�����܊w�|����
- �u�a�Z�̗��j�^�]�˂̐��w�v��������}����
�z�[���y�[�Whttp://www.ndl.go.jp/math/s1/1.html
- �g�c���R�u�o���L�v���^�� �Z���A��g����
- �R�����i�u�Z�@�����I�]�˂̐��w�ɒ���v�u�k��BlueBacks

��낵����A���̔���{�^���������ĉ������B
�i�����݂��ł��܂��j
�i�����݂��ł��܂��j